순열과 조합

2014년 한양대학교 이상화 교수님의 강의를 보면서 정리한 것입니다.

Permutation(순열)

• $n!$

  • n개의 element를 일렬로 나열할 때의 경우의 수

• $ _nP_r = \frac{n!}{(n-r)!}$

  • n개 중에서 r개를 뽑아서 나열하는 경우의 수

• $0! = 1$

  • 아무것도 나열하지 않는 경우의 수는 한개니까 1이다.

• 예시: group permutation(중복이 있는 순열)

  • $n_1 + n_2 + ... +n_k = n, n_k:subgroup \space of \space n$

• $ N_K = \frac{n!}{n_1!n_2!...n_k!} $

  • 중복을 제거해주는 것이다.

Circular Permutation

• 원 순열은 각 element가 한칸씩 이동하여도 같은 것으로 본다. 그래서 $(n-1)!$이다.
  

  

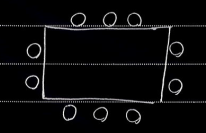
• 위와 같은 상황에서는 원순열에서 5를 곱해주면 된다.

Combination

• n개 중에서 r개를 뽑아내는 것이다. 순서는 고려하지 않는다.
  • $ _n C_r = \binom nk = \frac{_nP_r}{r!} = \frac{n!}{(n-r)!r!} =\space _n C_{n-r}$
• n+m 중에서 k개만큼을 뽑는 방법은 다음과 같다.
  • $\sum_{i=0}^{k} \binom ni \binom {m}{k-i}$
  • 즉, n에서 i개 뽑고, m에서 k-i개를 뽑는데, 0부터 k까지 i를 넣었을 때의 합이다.
  • 남자가 m명, 여자가 n명 있는 조합의 경우의 수 예시.

Binomial Theorem(이항 정리)

• $(a+b)^n = \sum_{k=0}^n \binom nk a^{n-k}b^k$인 것이다.
• 이거는 나중에 이항 분포를 증명할 때 필요하다고 한다.

Stirling's Formula

• $n! \approx \sqrt {2 \pi n}(\frac ne)^n$
• 이게 숫자가 어느정도 커지면 거의 같아진다는데... 계산은 더 빨라서 쓴다는 것 같다.

Reliability Application

• Reliability(신뢰도): 시스템이 유용하게 동작하는 기간
• R(t): 특정 시점 t까지 잘 동작할 확률
• 직렬 연결이면 $R(t) = \Pi_{i=1}^{n}R_i(t)$이다.
• 반대로 병렬 연결이면, $R(t) = 1- \Pi_{i=1}^{n} (1-R_i(t))$이다.
  • 적어도 한개의 module이 동작하면 된다. 전체 확률(1)에서 전부 다 동작하지 않을 확률을 빼면 된다.즉, 병렬 연결을 하면 R(t) 가 높아져서 좋다.
• 직렬과 병렬을 혼합한 복잡한 예제도 있다.